Quantitative analysis

Introduction

The analytical chemistry is:

that part of the chemistry that deals with
analysing, investigating of
chemical compounds and mixtures.

Analytical research is in our society indispensable. It takes an important position in the world of scientific, technical and medical enterprise:
Every day raw materials, products, waste, etc must be investigated on quality and quantity. Such investigation is done by all kinds of chemical industries (plastic, comsumption articles, fuels, metals etc.); in many enterprises the analytical chemistry has an important role.

Industries, of course, want know the need of raw materials, how much half products and product can be produced, etc. The analytical chemistry has a range of techniques and methods to provide this information. De complex procedures in the analytical chemistry are often realised within the factory labs.
Many things are continuously changing in the area of analytical chemistry, but many old methods still are used.

But also the government and the consumers organisation control on daily basis the quality and the composition of all kind of product available on the markets. Pollution of the environment and forensic research are just a couple of examples. You might think of measruing the pollution of rivers or drugs, but also the controle of DNA material, etc.
The application area is immens.

Simply reviewed, we can say that it is all about measuring:

"what is in it and how much of that."

We can divide the chemical analysis in two kinds of research:
1	The qualitative analysis:	wich substanc(es)?
2	The quantitative analysis:	how much of every substance?

Part 1, the qualitative analysis has been treated in module 13.
This module 14 is all about the quantitative analysis.

Content

1. Atom mass

2. MOL

2.1 Convert units

2.2 Element analysis of carbon compounds

3. Concentration / Molarity

4. Determination of molecular mass

4.1 Method I

4.2 Method II

5. Reaction calculations

5.1 General

5.2 Titrations

6. Use of p-values and
important constants

6.5 Solubility product K_S and solubility S

7. Action tasks

1. ATOM MASS

Question 1, to remember module 1:

How was that again with the mass of one electron compared with nucleons?
Is there any difference between the mass of a Calcium atom and a Calcium ion?

Mass of atoms

Particle	Mass (g)	Mass (a.m.u)	Charge
Electron	9,1*10^-28	0	-1
Neutron	1,67495*10^-24	1	0
Proton	1,67254*10^-24	1	+1

Att.:
The mass number of an atom equals the total number of nuclear particles (nucleons).
The atom number of an atom equals the number of protons is the nucleus.

The mass of electrons can be neclected, compared to the mass of nucleons (protons and neutrons). To determine the mass of an atom, you only need to count the number of nucleons: than you get the mass number. That's why an atom will/must have the same mass as its fellow ion. That ion only has one or some electron extra or short, and they weigh about nothing.

Question 2
Based on the table before, how many times heavier is a proton compared with an electron?

Question 3
In a nuclear reaction, a neutron can transfer into a proton + an electron (β-radiation).
Controll with help of the above table if, and how the masses do change during this transformation.

The atomic mass unit = a.m.u. = 1 u(nit)

Question 4
Using the definition of a.m.u., you must prove that the a.m.u. can be considered as the average mass of one nucleon.
Calculate the average mass in grammes.

Question 5
Suppose that you have 1 g of nucleons (a mixture of protons and neutrons).
How many nucleons do you need for that? (use the above table)

Isotopes

also read module 01
Every atom has its own mass number: the sum of the nuclear particles.

The Cl atom has 17 protons and can have 18 neutrons, or: the mass number of this Chlorine atom is 35.

Any element can have various isotopes, particles with equal atom number, but different mass number. The average atom mass must be based upon the proportion between those isotopes.
The values of atom masses can be found in tables, like table V, column 4
The atom mass is based upon the mass number of de different isotopes of the element.

Chlorine, for example, has apart from atom 35, another isotope with 20 neutrons, so with mass number 37.

The average is not 36, because in nature there is three times more ³⁵Cl than ³⁷Cl.

Finally you can calculate that the average atom mass of Chlorine must be about 35.5

It is calculated that 6.10²³ nuclear particles (toghether weighing 6.10²³ u), have a total mass of one gramme.
1 gramme contains: 600.000.000.000.000.000.000.000 nuclear particles (nucleons, meaning the protons and the neutrons toghether)

Question 6
Explain that the average mass of one nuclear particle equals 1,7.10^-²⁴ gramme.

2. MOL

Such small amounts of mass, of course, cannot be weighed on any scale, but only determined indirectly via complicated apparatus.
In chemistry the enormous number 6.10²³ has become a standard number and is frequently applied. The first who invented and used it, was Avogadro. So the number is also called:

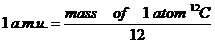
< Number of Avogadro = 6.10²³

Two new units for masses or amounts have been introduced in chemistry:

one micro-unit for the very small particles (atoms, molecules, ions, electrons). This micro-unit is a unit of mass: the 'atomic mass unit', amu, or: UNIT
one macro-unit for such big numbers of small particles that they can be weighed on a normal scale. This unit, MOL, is a unit of numbers.

< One MOL is 6.10²³

Question 7
Keep in mind the following numbers: a pair, a dozen, a gross, a mol; Explain that it is nonsens to imagine one mol of people.

N.B.
Note that you should not confuse the chemical concept mol with the biological mole.
We write both MOL and mol.

Because electrons do not contribute to the atom mass, the mass of atoms is concentrated in the nucleus. Knowing the number of nuclear particles, automatically you know the mass of that atom in U(nits).
Then taking one MOL atoms of that substance (6.10²³ atoms), you know the mass of it in grammes.

Example: Calcium (http://nl.wikipedia.org/wiki/Calcium)

Calcium (⁴⁰Ca) has 20 protons and 20 neutrons; toghether 40 a.m.u.
1 atom of Ca weigh 40 u.
6 x 10²³ atoms of Ca weigh 6.10²³ times more;
1 mol of Calcium atoms weigh 6.10²³ x 40 u = 40 gramme

In the table you find the value of atom mass of Calcium 40,1 (consequence of isotopes).
40 is the number of nuclear particles of a normal Calcium isotope with 40 nucleons.
Now applying the number 40,1 (atom mass) in micro and on macro level:

one atom of Calcium weigh 40,1 u(nits){micro level}
one mol of Calcium weigh 40,1 gram {macro level}

Question 8
Zinkum and Copper molten toghether gives brass.
zie: brass

Explain how much will weigh 1 mol of Zinkum + ½ mol of Copper (brass), on micro as well as on macro level.
Make sure that you can read the data of table V on micro and on macro level.
How much will weigh: 1 mol of sugar; ½ mol of water; 10³ mol of H₂?

2.1 Transformation of units.

In practice we often work with the units: (milli)gramme, kilogramme, ton, in particular when working with solids.
Working with liquids, and certainly when working with gases, we need units of volume: liters (=dm³), milliliters (ml = cm³), m³. You must be capable to work with these units, easily and quickly.
Study the scheme below:

Molberekening (45K)

Question 9
How many mg is 1 ton? How many literis 1 ml? You must be able to execute these kind of conversions by heart and fast.
Believe me. Train a lot please.

At physics you have learned that in case of solids and liquids you can relate mass and volume. For that you use the density.
The used unit in tables can be read in three ways: ton/m³ = kg/l = gr/ml (above and below the dash the amounts become every time 1000 times smaller.

1 liter of alcohol weight 0,8 kg, but also:

1 ml alcohol weigh 0,8 gramme (= 800 mg).

Question 10
How much weigh 10 l of petrol, and how many mol are they? (formule: C₈H₁₈(l); density=0,72)

To know the volume of a gas, in particular the volume of one mol of that gas, then the calculation is different.
There is a fundamental difference between gases on one side and solid / liquids on the other side: The most special characeristic of gases is that all gas particles are lose from each other and that therefore the volume of a gas does not depend on the size of the gas molecules.
The issue is: how far are those molecules separated from each other? How big is the distance between the molecules? What's the distance? That's what counts.

in solids en in liquids, all molecules close toghether, wether moving or vibrating or quiet. So in (s) or (l) the first question is: how big are the molecules? The bigger, the more volume they need.
But with gases totally different.

The volume of a gas, in fact the mutual distances between the gas molecules, in the very first place is determined by pressure and temperature:

At higher pressure the gas molecules are forces closer toghether and the mutual distances are smaller, and you have more molecules per liter, i.e. more mols per liter. That will make a gas with high pressure also heavier.
At higher temperatures (i.e. the gas particles move faster and with higher rate) the molecules will have more distance. then you will have less molecules per liter, or less mol/.
A liter hot gas is also lighter then a liter cold gas.

At 0°C and 1 atm. pressure, the volume of 1 mol gas = 22.4 liter, no matter what gas. At another temperature and pressure that volume is different, but for any gas the same at the same conditions.
for example: at 100°C every gas has a volume of about 27 liters.

There is a general gas law. With that you can calculate how many liters make one mol gas, at a defined temp and pressure. We've got for that mathematical formulas.

Taking an equal volume of two gases with the same temp and pressure, then the same number of moles is found as well as the same number of molecules, whatever gas you consider.

When changing units in chemical calculations, the concept of MOL always is in the centre. You must learn the scheme below, and know how to apply it:

Question 11
A certain car goes 15 km with 1 liter of petrol.
How many mol of petrol must be burnt for a ride of 200 km?

Question 12
How much is the mass percentage of C and H in natural gas?

Question 13
Find the needed data in the table below, giving the solubility of a gas in water:

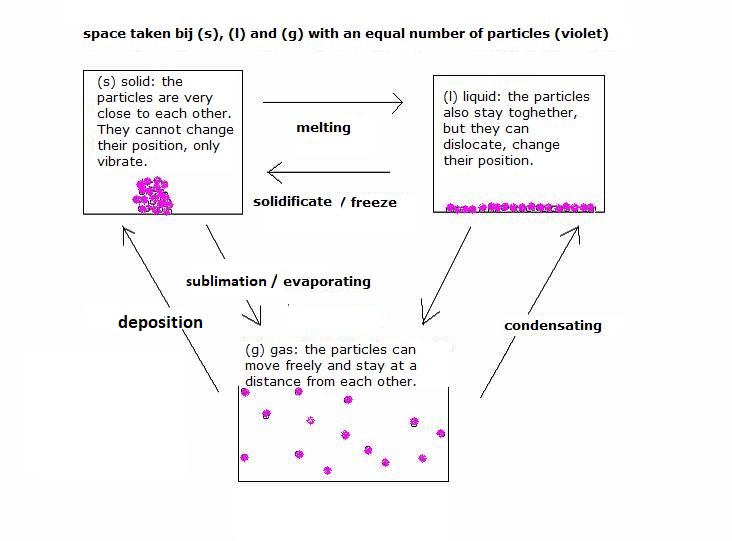
	CO₂	O₂	NH₃
0°C	75·10^-3 mol/l	2·10^-3 mol/l	52 mol/l
25°C	34·10^-3 mol/l	1·10^-3 mol/l	26 mol/l
100°C	0.0·10^-3 mol/l	0.7·10^-3 mol/l	0.0

Bereken m.b.v. de tabel hoeveel gram koolzuurgas er opgelost is in een halve liter verzadigde oplossing van 25°C.

Question 14
How much water can be found in 500 g cristal soda?

Also plastics, nylon, polyesters, polyethers etc. are built up of molecules.
The molecular masses of these molecules vary between 10.000 and 1000.000.
We've got here very large molecules: MACROMOLECULES

In classroom must be demonstrated how you make 0.1M NaCl, and what instruments you need for that.
You must at least know the following concepts:

skale (for weighing)
pipet
graduated flask(zie ook flask)
buret (zie ook buret)
graduated cylinder (see also cylinder)
graduated gas seringe

also study the photographs below of glass work:

2.2 Analysis of elements in Carbon compounds

A carbon compound (organic chemistry) always contains the element C, often H and sometimes O.
Here we leave other elements like N and S out. The formula of the substance to investigate could be, for example: C_xH_yO_z

In the analysis of elements, you must determine the amounts of C and H in (milli)grammes.
Because you measured the total mass of the substance beforehand, you automatically can see if Oxygen was present, and, if so, how much.

You weigh very carefully and exactly a certain amount of the substance to be analysed (a monstre).
Then this substance must be burned completely; all C is transferred into CO₂ and ll H into H₂O.
The amount of Carbon dioxyde and water must be weighed.

From the amount of carbon dioxyde can be calculated the amount of C
From the amount of water can be calculated the amount of H

If the original amount of substance is more than C + H toghether, then there must have been Oxygen in it.
Now you can check of Oxygen was present in the original substance; if so, you can write that amount.

Now you know the mass proportion C : H (: O)
That mass proportion must be transferred into the mol proportion, by dividing by the atom masses of C, H (and O).
In that way you get the proportion x : y : z

Question 15
Explain that this way you only will get the proportional formula (C_xH_yO_z)_n and not the real molecular formula C_xH_yO_z.

The carbon dioxyde and the water that must be determinde in this analysis of elements, can be captured and weighed as follows:

First the water(g) is captured by a hygroscopic substance that was weighed before the experiment.
For that you could apply: waterfree Calcium chloride or waterfree Copper(II)sulfate.
Then the carbondioxyde is captured by, for example, a strong base like Calcium hydroxyde.
Again that must be weighed before and after the experiment. The difference is the captured gas.

Question 16
Someone burns 100 cc of petrol in an excess of dry and pure Oxygen.
The combustion products are sequently brought through waterfree Calciumchloride and through Calciumhydroxyde.
The tube with the Calcium hydroxyde became 220 gr heavier and the Calcium chloride tube 102 gr heavier.
Then 10 cc of petrol is dissolved in 100 gr of aceton; this causes a boiling point of 57.40 °C.
Determine the molecular formula of this petrol.

3. CONCENTRATION & MOLARITY

All mixtures are composed of two or more components. If the components cannot be distinguished from each other, we call it homogeneous. All particles in the mixture are divided very equally amongst the space.
This is always the case if the mixture is composed of gases, for example: air.
If one of the components is (l) and this mixture is transparent (not trouble), then you've got a homogeneous solution, for example sugar water. The liquid component fills the whole space and is the biggest part of the mixture; then this is the solvent. The other component(s) is(are) the solute(s) that apart can be (s), (l) or (g).

If the particles of a component are not equally divided in the space, then we have a heterogeneous mixture.
examples: chalk in water, smoke, oil + water, foam.

Only if the particles of a component are equally divided in the space (homogeneous), we can calculate the concentration of it: every liter of the solvent contains an equal amount of molecules of solute, no matter where you take that liter out of the mixture.

Question 17
Can you determine the salt concentration in sea water? yes or no. idem for sand concentration in mud?
Explain your answers.

For hetergeneous divided substances we cannot calculate any concentration.

In chemistry we take as a unit of concentration mostly: mol/liter = mol.l^-1
If we want to indicate the concentration of a substance in a mathematical formula, we do that with square brackets: [NaCl]; [O₂]

Another frequently used word for mol/liter (concentration) is molarity, often indicated with .....M.
Suppose that you have a salt solution with a concentration of 0,4 mol HCl per liter water, then you say: this salt solution is 0.4 molar;
The molarity is 0,4 or, in writing: 0.4M HCl.

Question 18
Explain what is meant by: 10^-4M CO₂

If the concentration of a solution is known, and also the amount of solute, then you can calculate the total amount of present solute.
10 ml 0.1M HCl contains 0.01 x 0.1 mol HCl (10 ml=0.01 l)
5 liter 0.02M NaCl contains 5 x 0.02 mol NaCl

Question 19
Calculate how many grammes of sugar are present in one cup (100 ml) 0.3M sugarwater.

At concentration calculations you always must give attention to at least two substances:

the solute is given in mols.
The solvent is given in liters.

Apart from that, you must know how to transform mol to mmol, from liter to ml, and v.v.:
1 ml = 10^-3 l
1 l = 10³ ml
1 mol/l = 10^-3 mol/ml

Question 20
Fill out:

0.4M NH₃ = ....... mmol/l
10 ml 0.2 M NaCl contains ..... mol NaCl

Question 21
A trade solution of hydrochloric acid contains 38% pure HCl. The density is 1.2 g/ml. The molarity is 12.
Suppose someone buys 100 kg of that trade solution.
How many HCl molecules are solt then?

When something is analysed in chemistry, often the concentrations of many investigated substances seemt to be far below 1M, for example: 10^-3M 3.10^-9M etc.
To calculate fast and easy with such low concentration, chemistry uses the so called p-values. In a mathematical way this means: -log; Just leave out the sign and the the basic numver 10:

p..... = 3 means: [.....] = 10^-3 mol/liter

Question 22
So what means:

pNaCl = 2
pNH₃= 6

It also happens that the substance itself is abbreviated; charges are left out, sometimes even more:

pH = 5 means: [H₃O⁺] = 10^-5 mol/l
pOH = 7 means: [OH^-] = 10^-7 mol/liter

Now try (if possible) to execute action task A, to be found at the end of this module.

4. DETERMINATION OF MOLECULAR MASS

Remember?:

Micro level: 1 molecule of any substance weigh M u(nit).
Macro level: 1 mol of any substance weigh M gramme.
1 u(nit) is the average mass of one nuclear particle.

Weighing directly one molecule is impossible, so Molecular mass M must always be determined indirectly.
Weighing one mol is possible, but for that the molecular mass M must already be known.
The purpose is now to know how to determine the molecular mass of a substance.

The determination of M of an unknown substance often starts with carefully weighing of a certain amount of grammes; to be used during the determination.

Question 23
Explain why determination of a molecular mass always is done with unknown substances; and explain why you need that substance in absolute pure form.

For a good experiment you need a homogeneous substance, very regular divided inside a certain space.
The applied method depends on the phase of the substance:

method I is applied when the substance is (s) or (l).
method II is applied when the substance is (g).

If the substance is (s) or (l), the molecules must be divided homogenous.
In order to realise that, the substance...:

must be dissolved in a propriate solvent; of that mixture (the solution) you must determine the freezing point (f.p.) or the boiling point (b.p.).
(Method I)
must be evaporated.
(Method II)

4.1 Method I:

Dissolved substances influence the f.p. and the b.p. of a solvent; a liquid will freeze or boil more difficultly when strange particles are present in that liquid.

Question 24
Mention two examples of influencing f.p. in cold winter times daily life.

When freezing, always a lattice is made (for example, an ionic lattice).
The formation of a lattice is more difficult when strange (not fitting) particles are present, come into that lattice. So if a substance is dissolved in a liquid, it becomes more difficult to solidifacate that liquid. The realisation of a lattice has become more difficult.
In order to make, nevertheless, a lattice, you need a lower temperature: FREEZING POINT DECREASE (f.p.d.)
When boiling a liquid, the molecules at the surface of that liquid have to escape.
When strange particles of a dissolved substance are present, then the occupy a part of the total surface.
That's how it becomes more difficult for solvent molecules to escape from the liquid: BOILING POINT INCREASE (b.p.i.)

These effects (fpd and bpi)do not depend very much of the character of the dissolved particles (it is not very important what kind of particles were dissolved, like ions, atoms, big or small molecules), but depent in particular on the amount of dissolved particles (number of moles).

Note that at these determinations we do not use the usual unit mol/liter, but mol/100 g solvent. Don't ask why! Has something to do with history.
The amount of unknown substance (for example p grammes) is dissolved in a weighed amount of known solvent (for example q grammes).
After measuring carefully the f.p. or the b.p. of the mixture (using for example a very accurate Beckmann thermometer), and knowing the f.p. or b.p. of the pure solvent, than you can know the fpd or bpi.
The (unknown) molecular mass of the dissolved substance is M.
The number of dissolved particles is p/M. Thsi number of mols determines the decrease of increase.
Question 25
Imagine that the found M is 58,44 u, and you also know that the substance is built up of ions, what substance could it be?
And of what particularities you must think when determining the number of mol particles?

The number of dissolved particles is p/M. This number of mols of particles determines the increase of decrease.
The number of mols of solute is proportional with the fpd or bpi.

b.p.i / f.p.d. ≡ number of mol of solute

The real amount of solvent in practice rarely will be exactly 100 g; if you take less, then the effect will be stronger; if you take more solvent, then the effect will be less.
Suppose you take q grammes, then a correction factor is needed: 100/q

b.p.i. / f.p.d. ≡ number of mols of solute x 100/q

To make the step to an =sign, a constant must be introduced: K*.
This constant K* is called: the molar b.p.i. / f.p.d.
The value of K* is different per solvent and can be fount in tables.

Question 26
The molar bpi of water is 0.5; of benzene is 2.5
the molar fpd of water is 1.9; of benzene is 5

At what temperature will water freeze when 1 mol of substance is dissolved per 100 g water?
Idem for the solvent benzene.

If a substance is built up of ions, then this substance will dissociate in water in several particles (n particles)

f.p.d. or b.p.i. = K* x number of mols of solute x 100/q · n

or:

f.p.d or b.p.i. = K* · p · 100 · n
M · q

Question 27
25 g. stearic acid is dissolved in 100 g alcohol.
Determine (if apparatus is there) the b.p. and thus the bpi, and determine the molecular mass of stearic acid.

Question 28
A mixture of 5.14 mg of a substance Y and 251 mg phenol has a f.p. of 38.53^oC.
Calculate the molecular mass of Y.

Question 29
5 g of a salt is dissolved in 50 ml water.

Determine (if apparatus is present) the f.p. of this mixture and thus the fpd.

Calculate the molar mass of the salt.

4.2 Method II

When the substance is (g), then you have automatically a homogeneous substance; a gas is always homogeneous divided in space.
Here also we have to weigh: a certain volume of gas is weighed at known temperature and pressure.

Question 30
Explain or find out how you can weigh a gas.

Then you must weigh a same amount of Hydrogen gas at the same temp and pressure. You can calculate now how many times heavier the unknown gas is compared with Hydrogen.

Question 31
Explain why the gases X (the unknown one) and H₂ must be weighed at equal temp and pressure.

If you know that the unknown gas is x times heavier that Hydrogen, then we call that number of x: the gas density D_H.

Definition:

D_H = mass of V liter gas (at t and p)
mass of V liter H₂ (at t and p)

Don't forget that for gases at equal t and p always the same volume has the same number of molecules, then you can derive from that definition the following formula:

D_H = M(gas)/M(H₂)

or rather:

M = 2D_H

Question 32
Derive this formula from the definition.

Question 33
You must investigate an unknown substance X(s).
Dissolving X in chloric acid, a gas A is formed.
One liter of that gas A is weighed: 1.98 gramme.
An equal amount of Hydrogen at the same t and p weigh 0.09 gramme.
Next to do is taking 10.6 g of the substance X, and dissolving it in 400 ml water.
The freezing point turns out to be -1,4°C.
Try to find what substance can be X.

5. REACTION CALCULATIONS (see also module 7) When, long time ago, Jules Verne wrote his great voyage to the moon, he described exactly how much gun powder was needed to empower the "rocket" with the crew to leave the earth, how much of the chemicals should be taken with them, the exact amount of Oxygen needed for those men during the planned days of the trip, etcetera.
If today something like that really happens, a similar calculation has still to be done with the same accuracy or better.
For example: a solid rocket fule is hydrazine, made of ammonia (to be calculated in liters of gas) and Sodium hypochlorite (to be calculated in grammes. Toghether they react and produce the right amount of hydrazine and no reactants are left over.

Question 34
Somebody wants to set up a soap factory. He needs for the process: vegetabel oil, kitchen salt, Sodium hydroxyde, water, energy, buildings, etcetera.
Give a short survey of the plan of operations.

Another example:
If in a sulphuric acid works, sulphur dioxyde(g), oxygen(g) and water(l) is mixed to produce sulphuric acid, then the amount of every needed reactant is calculated very precisely.

There are so many applications. Any factory starts the production with a well balanced reaction equation in order to calculate how much product can be made from how much reactant.
Not doing so, mixing some reactants arbitrarily, gives the big chance that wrong products and side products wil appear, and secondly, that much reactant gets lost; economically (and environmentally) this would be desastrous, cost a lot of money, etc.
The good manager looks for someone that knows about reaction calculations.

5.1 General

Demonstration at school, or in a lab:
x g Magnesium is dissolved in 1M HCl.
The produced gas is collected and measured in a gas seringe.
Starting with that known amount of gas, measured at room temperature, must be calculated how much Magnesium was dissolved in the acid.

Preparing a chemical reaction, it is important the you know how much of the reactants is needed and how much of the products you can expect. This is not only a chemical, but also an economic interest.

Always atoms, molecules, ions collide when reacting; these particles can be very different in size and in mass (but not necessarily).
Thus a big and heavy atom can very well react with a very tiny ion. Of course this is reflected in the 'mass proportion'.

For every reaction one thing is clear: whatever amount of atoms, molecules or ions you bring toghether, they will always react in a fixed proportion. That fixed number can be read in the coefficients of the balanced reaction equation.
The coefficients in the reaction equation have two significations:

the micro meaning: number of ions, atoms etc.
the macro meaning: number of mols

In the reaction: 2H₂ + O₂

2H₂O the coefficients mean to say:

(micro): 2 molecules of Hydrogen react with 1 molecule of Oxygen and produce 2 molecules of water.

(macro): 2 mol of Hydrogen react with 1 mmol of Oxygen and produce 2 mols of water.

The proportion 2 : 1 : 2 is a fixed one and is called: the mol proportion.
A reaction calculation always starts with a well balanced reaction equation.

Question 35
Show in what mol proportion Calcium and water react, and calculate in what mass proportion these substances react.

Note that the proper reaction determines the coefficients. The coefficiebnts do not depend on the amount of substances available.
Even if you mix 100 mol Hydrogen with 1 mol of Nitrogen, the mol proportion of this reaction wil remain the same:

N₂(g) + 3H₂(g)

2NH₃(g)
so
1 : 3 : 2

Question 36
Explain that in the above example not more than 2 mol ammonia can be produced.

Substances built up of ions (mostly to be recognized with the fact that there is a metal present in the compound) in dissolved state, are split up, dissociated into ions; in solid state they have an ionic lattice.
In reaction calculations mostly counts the amount of not dissociated substance, needed or produced. That's why equations for calculations are written in proportion formulas, not in ions. that is easier for the calculation.
You do not weigh loose ions, don't you. We don't have bottles with only Sodium ions.

We write in ions: Na⁺ + Cl^- + Ag⁺ + NO₃^-

Na⁺ + NO₃^- + AgCl(s)

We write in proportion formula: NaCl(aq) + AgNO₃(aq)

NaNO₃(aq) + AgCl(s)

In chemical calculations, the last way of writing is preferred.
Always add the state of matter (the phase): (s) (l) (g) (aq). This can prevent many mistakes.

The reactants react in a fixed mol proportion; when they are not mixed in the right proportion, they react as long as there still are both reactants, until one of them is totally consumed.
The rest remains unchanged.

Question 37
Imagine that you burnt 1 g of Sodium in 100 liter of air.
Calculate how many g product are mad and how many liters of oxygen gas will remain. (0ºC, 1 atm.)

For gases and for liquids we often use a unit of volume: liters or mls.
Transforming these units into other units might be necessary. We often use the 'density' to transform volume into mass or v.v. The volume of a gas can also directly be translated into mol (knowing the t and p).

Question 38
Calculate how many liter of Hydrogen will be produces when 10 g of Calcium is dissolved in sufficient water.
The gas is measured at 0ºC and 1 atm.

It is wise, for good understanding of the practice, to indicate the state/phase (s), (l) of (g) (or (aq)):

Ca_(s) + 2H₂O_(l)

Ca(OH)_2(aq) + H_2(g)

This calculation is also an example to show the advantage of using the proportion formula (or empirical formula) more than ionic formulas.
Chemical calculations deal with real stuff, and ions alone cannot be dealt with.
So even when only the Chloride ions participate, yet you must weigh kitchen salt (NaCl).

N.B. Remember the equation: d = g/v?

Gases also have a density, but gas density has a complete different definition than density of (s) or (l).
Good to know about gases:
Whatever gas you take, with big or small molecules, one mol of it always has the same volume, measured at the same t and p.
In other words:
If you take on liter of a gas, measured at a fixed t and p, than whatever gas you take, that liter contains the same number of mols.
Mol and volume are proportional in the case of gases.
What is absolutely not true for liquids and solids, is true for gases: the coefficients of gases in an equation can be read as mols �nd as liters or ml.

For gases: MOL PROPORTION = VOLUME PROPORTION

Question 39
What volume has 1 mol of gas at a pressure of 1 atm and a temp of 0ºC?

If methane reacts with Oxygen in the proportion 1:2 (one mol methane react with 2 mol Oxygen), this means that at the same time automatically and under the same conditions 1 liter of methane gas react with 2 liter of Oxygen gas.

Example:
What is the mass and the volume (standard circumstances) of Carbon dioxyde produced in the complete combustion of 4.01 g Methane?


1	CH₄(g) + 2 O₂(g) CO₂(g) + 2H₂O(g)
2	Subline those substances about which you have data, or about which is a question. CH₄(g) + 2 O₂(g) CO₂(g) + 2H₂O(g)
3	So, 1 mol CH₄(g) reacts with 1 mol CO₂(g) (proportion is 1:1)
4	16 g CH₄(g) produce 44 g CO₂(g) (here we apply the molecular masses)
5	in reality we have not 16 g, but only 4 g to be burnt. The factor to be introduces is: 4/16. 4/16 x 16 g CH₄(g) produce 4/16 x 44 g CO₂(g) finally: standard circumstances mean: at temp 25°C and pressure 1 atm. Then 1 mol gas = 22.4 liter 1/16 x 44 = 11 gram CO₂(g) is produced, that equals 4/16 mol = 4/16 x 22.4 liter CO₂(g) = 5.6 liter

Question 40
1 gram Sodium is burnt in 100 l of air (0°C and 1 atm.).
Calculate, in grammes, how much oxygen remains.

Question 41
Ore of Iron contains 75% iron(III)oxyde. Calculate the mass of the Iron that can be made out of 1 ton of the ore.

Question 42
Someone uses natural gas (methane) to boil water during 15 minutes, in order to kill bacteria.
She consumed 5 g of gas.
Calculate the mass, in grammes, of the needed Oxygen for the whole process.

Question 43
To burn 1.3 mol of natural gas, how many mol of Oxygen are needed? (all measured at equal t and p).

Question 44
Calculate the amount of ammonia and Oxygen (in grammes) needed to produce 3.00 g of NO. A side product is water.

Question 45
Concentrated sulfuric acid contains 96% pure H₂SO₄. The rest is 4% water.
Calculate the number of mol H₂SO₄ in one liter of concentrated sulfuric acid, knowing that the density of it is 1.84 g/cm³.

Question 46
3 mol of Chlorine and 150 g of Iron react and produce Iron(III)chloride.
Which substance is the limiting substance (will be completely consumed?): Chlorine or Iron?

Question 47
Nitrogen and Hydrogen react in a direct reaction with each other and form the product ammonia, in an industrial reactor with a catalyst.
1000 g of the product is made a yield of 97.8%
The molecular mass of ammonia = 17.0
How many mol reactants are needed?

5.2 Titrations

In a lab or in the classroom should be demonstrated and discussed a simple acid base titration + calculation.
This could be done as follows:

First the titration is executed with a pH meter and a plotter, when the titration liquid (titulant) is added regularly dropwise from a buret, until passing the end point.
Then the titration has to be repeated with an indicator to stop exactly in the end point.
Finally, the calculation must be done and discussed.

On internet you can find nice examples of titrations, for example: Titrations on wikipedia

Question 48
25 ml Potassium hydroxyde(aq) with unknown concentration is titrated with 16 ml 0,27M HCl.
Calculate [KOH].

A titration is a rather fast method to determine the concentration of dissolved substances.
We use certain apparatus where the volumes of liquids can be read accurately, like: pipettes, burettes, graduated flasks, and more.
That's why we also talk about volumetric analysis.

The reaction equatiopn shows the mol proportion of the reactants.
When the reactant are joined exactly in that mol proportion, we say that the equivalence point has been reached.

Question 49
Calculate the equivalent amount NaOH for 0.3 mol sulfuric acid.

In most cases of titration, two dissolved substances react carefully; the addition is stopped, if possible, exactly at the moment of equivalent amounts of reactants.

Question 50
10 ml tri-Iodine solution (I₃^-) is titrated with 23.9 ml 0.1M tiosulfate (S₂O₃^2-).
How many grammes of Iodine (I₂) contained the original solution per liter?

The concentration of the titulant (mostly in the buret) must be well known.
The concentration of the other substances can be calculated, starting with the data.

At the moment of having joined equivalent amounts of substances, the reaction must stop; so stop adding from the buret at that very moment.

Normally we stop this process just a bit too late; with the last added drop of titrant solution a bit too much was added.
The practical end point of the titration in many cases does not coincide 100% with the theoretical equivalence point. We add automatically a bit too much.
For a reliable determination, this error may not be more than 0.5%. In practice this means that you may add at most one drop too much on a total of 200 drops.

Question 51
In a titration, 3 ml titrant solution was added from the buret (about 60 drops); suppose you added half a drop too much, is your titration accurate enough?

To be able to observe the endpoint, the changing moment, we often need an indicator
At acid base titration:	an acid base indicator
At redox titration:	a redox indicator

An indicator mostly is....:

a weak organic acid	a weak organic reductor
HIn H⁺ + In^-	Red_In n e^- + Ox_In
HIn has another color than In^-	Red_In has another color than Ox_In
The color of HIn or In^-	The color of Red_In or Ox_In
can only be observed if the equilibrium is sufficiently to the left or the right.
The color of an indicator depend on the environment: In acid environment (or in reducing environment) the above equilibria are at the left, so the color of HIn dominates (or the color of Red_In). Per indicator this can vary substantially.

For data about more indicators, you can find table VIII.

Question 52
Explain what color phenolred will have in KOH(aq); is the indicator molecule then neutral or negative?

Question 53
Explain what color methylene blue will have in a solution of Sodium sulfite; has the indicator molecule the Red- or the Ox-configuration?

At acid base titration, the pH of the end solution not necessarily must be 7; the end pH depend on the properties of the products.
These products can contain, in their turn, weak acids or bases.

The following fundamental rules can be applied:

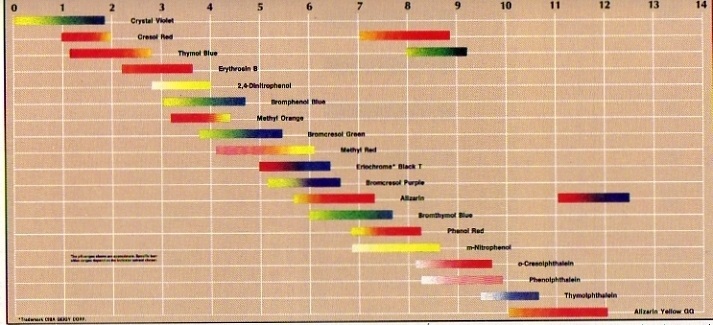
titration of strong acid with strong base:	pH = 7
titration of strong acid with weak base:	pH < 7
titration of weak acid with strong base:	pH > 7

Question 54
Explain why at the titration of acetic acid with KOH the end pH is > 7.

The right choice of indicator depend on the properties of the products �nd of the changing zone of the indicator (see table VIII).
The indicator must match with the titration.

Question 55
Explain wether or not the indicator methylorange suits the titration of acetic acid with KOH.

indirect titrations

Sometimes it turns out to be impossible to determine the concentration of a certain substance by titration; for example when such a substance is unstable of not soluble.
In such cases we can execute a so called indirect titration.
The substance to be determined must react beforehand with another reactant (en intermediate or a substitute). The original substance finally does not participate in the actual titration.
The substitute is titrated and its number of mols calculated.
after that, by calculating, you can determine how much original substance was present.

example:
Marble has a high percentage of Calcium carbonate, and you want to determine that percentage.
An option is to add a substance that reacts with the Calcium carbonate, so to remove all carbonate.
Imagine that you would use Nitric acid to do so; make sure that uyou know exactly how much nictric acid you added at the start. Part of that acid will react with the carbonate, a rest of it remains.
So, if you know how much acid you added in the beginning, and you know how much acid is left, then the difference is exactly the amount of acid that reacted with the carbonate.
The acid that remained can be determined by titration with a base, could be: NaOH(aq).

Question 56
You weigh exactly 10 g of marble and put this into 150 ml 1.0M Nitric acid. The produced gas must escape completely, by heating.
After that, you titrate the remaining nitric acid with 0.20M NaOH; needed: 10.0 ml
Calculate the percentage of Calcium carbonate in the marble.

Often we use, in the case of redoxtitrations, the couple: I₃/S₂O₃^2-(Iodine with tiosulfate).
This titration mostly is applied at indirect titration: the substance to investigate is replaces by Iodine or Tio, dependent on the question: was the unknown substance an oxydator or a reductor?
At these so called Iodometric titrations we use the cheap and well working indicator: starch(aq).
Fresh starch has spiral shaped molecules (see also module 12, biochemistry), wherein the tri-Iodide ions exactly fit and cause a dark blue color.
the tri-iodide itself also has a color (yellow brownish), but the (dis)appearance of that color is not as clear to observe as is the dark blue color

Question 57
Write down what you can observe if you titrate an Iodine solution with Tio using yes or no a starch solution as an indicator.

If you want to execute an acid base titration without any indicator, then you could use a pH meter. On the meter you must continuously check the (changing) pH values: In the equivalence point, the pH change is at its maximum; a sudden big pH change shows up.
You can plot the course of the pH change in a graph (by hand or automatically).

Every time you add, for example 0.5 ml titrant, you read the pH value, or the potential (in the case of redox reaction) and you put that value on paper. That's how you create a titration curve. In such a curve you can easily derive the equivalence point.

Question 58
What kind of end point determination is more accurate: with an indicator or with readable meters?

Question 59
What kind of acid base titration belongs to any of the four titration curves?
titratiekromme (18K)

There are several titration methods, partly already discussed, partly to be discussed later.

precipitation titrations
colorimetric titrations
acid base titrations
redox titrations
complexometric titrations
coulometric titrations
thermometric titrations

6. Applying p-values and importants constants

In various modules we used logarithms, negative logarithms and p-values.
Best is now to repeat that and do some exercise:

log10^-2 = -2 en ook:p10^-2 = 2
log 4.10^-2 = log4 + log10^-2 = -2 + log4 = -2 + 0,60= -1,40 and also: p4.10^-2 = p4 + p10^-2 = 2-log4= 2-0,60 = 1,40
pX = 3,7 = 4-0,3 = 4-log2,00 dus ook: X = 2.10^-4

6.1 pH

The reason that we work with negative logarithms (p-values) can be found in the fact that in chemistry the concentrations of substances often is very small.
Are you used to is, you will find that this is a very easy way of writing data:

pH = 6 instead of [H₃O⁺] = 10^-6 mol/l

or:

pOH = 8 instead of [OH^-]= 10^-8 mol/l

Always when you write concentrations, you must add the unit 'mol/l'. Working with p-values, this is not needed.

Question 60
Explain if the followint mixture is neutral: 1 mol H₂SO₄ + 1 mol NaOH

Question 61
Explain which of the two solutions has the lowest pH, and measure, if possible, the pH:

1M H₂SO₄ or 1M HCl
1M HCl or 1M HAc
0,1M HCl or 1M HAc

6.2 K_w

In module 9 was spoken of water as an ampholyte, so a very weak base �nd a very weak acid.
If no other substances are dissolved in water, than the pH of that water, at 25 degrees C is exactly 7 as also the pOH = 7.
With the (water)equilibrium (H₂O + H₂O

H₃O⁺ + OH^-) comes of course also an equilibrium condition K:

The waterconcentration is constant, does not change.

Question 62
Explain that the water concentration is about 55.5 mol/l and that the dissociation practically does not change anything.

From this you can draw a relation:

K.[H₂O]² = [H₃O⁺].[OH^-]

K·55,5 = K_w = 10^-7·10^-7 = 10^-14

Kw is called the water constant and is, at 25°C : 10^-14

As in all equilibria, also the water constant depends only on the temperature.

Question 63
Measure the pH of boiled water:

immediatly after the cooking
after complete cooling

The above formulas can also be written with p-values:

pK_w = pH + pOH

or in numbers:

pK_w = 14 = 7 + 7

If the pH and the pOH equal each other, so the [H₃O⁺] and the [OH^-] are equal, than the solution is neutral.

Because K_w is a constant (so pK_w too) pH and pOH toghether must be 14.

example: pH = 5 and pOH = 9. [att: only at room temperature!]

If the pH becomes bigger, the pOH becomes smaller and v.v.

adding acid makes the [H₃O⁺] larger, so the pH <.
adding base makes the [OH^-] larger, zo the pOH <.

6.3 K_A and K_B

If an acid (HA) or a base (A^-) is dissolved in water, than an equilibrium will be reached.
We can elaborate an equilibrium constant K for the acid as well as for the base in water:

Because the [H₂O] is constant (about 55,5 mol/l), this concentration is included in de constant K.

K_a is the acid constant
K_b is the base constant

Question 64

Calculate the pH of:

0,1M HAc

0,1M NH₃

0,1M HCl

the weaker an acid, the smaller the acid constant Ka.
The weaker the base, the smaller the base constant Kb.

(see also tabel I)

Question 65
Explain why strong acids and bases in table I have no acid of base constant.

A conjugated base belongs to an acid dat donated one proton.
In table I the conjugated acids and bases stand toghether. The difference between left and right is always one proton.

At 25°C the mathematical product of the acid constant and the base constant always will be 10^-14

Question 66
Check that in table I and prove that for the conjugated partners always: pK_a + pK_b = pK_w(=14)

Badly soluble salts (built up of ions with a very strong ionic lattice) where a base is present, will only act as a base if a strong acid is added:

Cu(OH)₂(s) + 2HCl(aq)

CuCl₂(aq) + 2H₂O

Cu(OH)₂(s) does not give any reaction in water to an indicator, becaus it is badly dissolved; the base (the hydroxyde ions)do not come free automatically.

Question 67
Explain the value of pH in a mixtyure of chalk and water.

If you must do a pH-calculation, do not start immediatly the calculation without looking well at the kind of substance you are dealing with; which particles ar present? Are there weak of strong acids or bases?
If you are dealing with an acid solution, always calculate with pH and/or with [H₃O⁺].
If you are dealing with a basic solution, always calculate with pOH and/or [OH^-].
As soon as you must fill in a concentration [...] in any formula (for example in K_a), than the unit must be mol/l. If needed, you must first do some conversions.

Question 68
Below you find some questions (68a - 68d) that can possibly serve as demonstrations.
They deal with joining well known amounts of acid and bases.
Of course you must first know if, and how they react.
As always in chemical reactions, one of the reactants will be consumed and of another reactant a certain amount will remain (unless you are capable to join them in equivalent amounts).
The way to resolve the problem is as follows:

Take care that you know exactly how much acid was used
Take care that you know exactly how much base was used
Investigate with a certained reaction equation which of the two will be consumed and which reactant will not completely disappear
Calculate how much will remain and convert this to mol/l
Continuously watch the volumes you work with.

the problems:

0,5 liter 1M H₂SO₄ is mixed with 0,5 liter 1M NaOH.
Calculate the pH of the final solution.
100 ml 0,05M H₂SO₄ is mixed with 100 ml 0,04M chalk water.
Calculate the pH before and after mixing. (25°C)
You might execute this experiment at 100°C.
90 ml H₂SO₄ (with pH = 2) is mixed with 10 ml sodiumhydroxide(aq) with pH = 12. the temperature is 25°C.
Calculate the pH of the final solution.
If possible, execute this experiment at 100°C.
50 ml 1M acetic acid is mixed with 50 ml 1M potassium hydroxyde(aq).
Calculate the pH of the final solution.

6.4 Buffer formula

Question 69
First calculate th pH of 1M acetic acid and calculate then the pH of a mixture of 1M acetic acid + 1M sodium acetate.

A buffer solution has the tast to keep the pH of a solution as stable as possible, even when strong acid or base are added.

In a buffer always are mixed toghether:
about the same amount of (weak) acid HA and conjugated base A^- The last one can, for example, be added in the form of well soluble NaA.
The HA aims to catch added base and the A^- aims to catch the added acid.
The more weak acid and conjugated base are toghether, the more strong acid and base can be caught and the bigger is the buffer capacity.

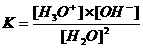
BUFFER:

A rather concentrated mixture of a weak acid with its weak conjugated base

In a solution of a weak acid always:
[H₃O⁺] = [A^-] (those two are set free in equal amounts from HA).
In a buffer however, lot of extra A^- is added, so in a buffer those two concentrations are no longer equal.

Adding to a buffer a littlebit of strong acid, the present weak base A^- will catch that added acid.

Question 70
Give the reaction equation for the adding of some oxonium ions.
(The [HA] will increase a bit; the [A^-] will decrease a bit).

Adding to a buffer a littlebit of strong acid, the present weak base A^- will catch (neutralise) that added acid.

Question 71
Give the reaction equation for the adding of some hydroxyde ions OH^- and explain how that will change the amounts of AZ en Z^-.

Adding to a buffer a littlebit of strong acid, the present weak base A^- will catch (neutralise) that added acid.

Adding a bit of strong base to a buffer, the present HA will catch (neutralise) that added base.

From the well known formula for Ka, you must be able to deduce the so called
bufferformula:

or:

Question 72
Answer the next three questions:

a mixture of hydrocloric acid and kitchen salt will be a buffer? Why (not)?
what pH has a mixture of 1 mol Sodium oxalate in 2 liter water?
what pH has a mixture of 1 mol Sodium oxalate + 1 mol SodiumHydrogen oxalate in 2 lieter water?

6.5 Solubility product K_S and solubility S

In table XI you can find of a large number of substances if they dissolve in water and, if yes, how much can dissolve befor saturating the solution.
For all substances, also for salts, there is a moment of saturarion.
Badly soluble salts reach that point much faster than well soluble salts.

The solubility of a salt mostly is indicated in the unit mol/liter, sometimes in mol/100 gr.

If a salt in water (partly) dissolves, than the ionic lattice (also partly) falls apart; the number of free particles increases.
Dissolving depends on the strenghth of the ionic lattice, but also of the temperature. At high temperatures the ionic lattice easier fals apart.

Question 73
Explain the influence of the temperature.

Badly soluble salts have ionic lattices that only dissociate in water for a (very) small part.
In that case there is a heterogenious and onesided equilibrium.

Question 74
Waht is that: a heterogeneous and onesided equilibrium
Give the equilibrium equation (including (s) (l) (g) (aq)) and the equilibrium condition for the dissociation of silver carbonate in water.

The small amount of silver carbonate that dissolves in water (in mol/l) is called the Solubility S at a certain temperature.
Att: in this example S mol silver carbonate will form: 2S mol silver ions and S ml carbonate ions.
The ions spread out homogeniously throughout the whole solution.
Because the solid and undissolved silvercarbonte is present in a heterogious way, the concentration of that solid in the equilibrium condition K may have the value 1.

Question 75
Explain that the equilibrium constant K for these badly soluble salts can be considered as: the ionic product in a saturated solution.

The ionic product (I.P.) in a saturated solution of a badly soluble salt is called the SOLUBILITY PRODUCT K_S

Question 76
Explain if K_s will be bigger of smaller at higher temperatures.

As long as there is not dissolved substance on the bottom, the solution saturated (I.P.= K_s).
If not, than you still can add and the solution is unsaturated (I.P.< K_s).
In special cases you can have oversaturated solutions (I.P. > K_s).

You must be capable to calculate S from Ks and v.v.: Ks from S.

Question 77
Now you must do some exercises with converting between S and K_s.

Calculate the solubility of silverchloride at roomtemperature in mol/l. [Ks of zilverchloride: 1,5 x 10^-10]
Calculate the solubility of silvercarbonate at roomtemperature in gr/l. [Ks of zilvercarbonate: 6 x 10^-12]
Calculate the solubility of silverfosfate at roomtemperature in mgr/l. [Ks of zilverfosfate: 2 x 10^-21]
Calculate the solubility product of leadchloride in water of 20^oC [S=2 gr/l]
Calculate the solubility product of leadchloride in water of 100^oC [S=25 gr/l]

ACTI0N TASKS

Action task A: reaction calculations

The following three experiments must be executed according to the six points of this action task:	Take notice, when working on it, that all you do, observe and think (about chemistry of course) and make at the end a report. Take care that the substance to investigate always remains in stock; never use all of it! Draw conclusions of every observation; that's how a lot of research will turn out to be unnecessary.
The 3 action points for every experiment are:	The 3 experiments are:
Weigh exactly about 0.25 g impure Calcium and dissolve that in a more than enough water (almost a full erlemeyer). The number of mls gas that is produces must be captured and measured with graduated gas seringe. Determine the purity of the Calcium in mass percentage. (at room temperature the volume of 1 mol gas: 26 liter). Weigh exactly a beaker with hot water.Cover the beaker. Weigh one tablet of soluble aspirine (headache etc.) and dissolve the tablet in hot water. After the reaction, weigh again the beaker + solution + cover. A component in the tablet is Sodium Hydrogen carbonate (NaHCO₃), another one is citric acid (H₃Ci). They are toghether in the right mol proportion. They react until both are gone. How much of the above mentioned substances were in the tablet? If the rest of the tablet is aspirine, how much aspirine is in a tablet? In cristal soda (Na₂CO₃.xH₂O), apart from Sodium carbonate, also exist cristal water. Weigh exactly about 5 g of soda and dissolve it in 50 ml water. Then add about 5 g (more than enough) Calcium chloride; stirr well and filter. The filter was weighed before the experiment and must be weighed again after. Note: before and after, the filter must be dry. Calculate now the amount of cristal water in soda (calculate x). (might be in stead of III.) You have a piece of Copper(II)sulfate of between 1 and 2 g. In this cristal is included cristalwater. Suppose that the formula is CuSO₄.xH₂O, then calculate x; invent a method.	Make a balanced reaction equation and indicate the phases. Subline those substances about which you've got information, data, or about which you must find out something. The other substances are not important for the calculations; leave them out. Dat can be given directly or indirectly. Execute the calculation just with the sublined substances. Point out the mol proportion. If it is possible to execute this reaction, do so. Where needed, you trasform mol into the needed units (to be found in data and questions) Introduce a calculation factor, respecting the real given amounts of substances. That's how you finish the calculation. Check your answer / estimate if the answer can be real, could it be reality?

Action task B: acid base reaction

Execute four experiments according to the four items of the task:	Every time write what you are doing, what you see, observe and what you think of it (in chemical terms of course), and make at the end a report. Take care that the substance to investigate always remains in stock; never use all of it! Draw conclusions of every observation; that's how a lot of research will turn out to be unnecessary.
the 4 action points for every task are:	The 4 tasks are:
Write the formulas of the (dissolved) substance: [molecular, proportion, ionic and electronic formulas]. Is there an acid or a base involved? If yes, which one? Prove that with an indicator. Execute the task and write al your observations. Write down all calculations and transformations you did during the calculation.	Pipet 10 ml vinegar and dilute it ten times in a graduated cycinder. Calculate how many molecules alcohol are present in those ten ml; calculate the alcohol concentration. Alcohol = ethanol = C₂H₅OH. Use the alcohol percentage indicated on the bottle. Wiegh 1/71 g sugar and calculate how many mol and how many molecules are there. Dissolve the sugar homogeneously up to exactly 100 ml water (in a graduated flask) and calculate the sugar concentration. (Suiker = C₁₂H₂₂O₁₁) Imagine a bottle with 1M Acetic acid; how many g of acid is there in half a bottle? By dilution, make about 0.01M acetic acit; put 10 ml of that solution in an erlemeyer; add some drops of indicator. From a buret, add 0.01M NaOH until color change. Read how many mls of NaOH were added. Bring exactly 10 ml xM HCl into an erlemeyer; add some drops of indicator. Add 0.01M KOH until color change.

Action task C: titrations

The aim is that your group will execute a number of the titrations below, according to the ten points of this action task, to be done in the right sequence:	During work, every time write down what you are doing, what you observe, what you think of it, and make a report at the end. Take care that the substance to investigate always remains in stock; never use all of it! Draw conclusions of every observation; that's how a lot of research will turn out to be unnecessary.
The 10 action points for every task are:	The 6 tasks are:
Make an ampel design to show what actions must be done chronologically. Put all data (formulas and other data) in the drawing at the right place. Write down with what substance will be titrated; what is the titrant? Which reaction type is applied in this titration? How could the end point been determined? Explain. Give all reaction equations at the right place in the drawing. Execute the titration. Was it a direct or an indirect titration? Start the calculation with the molarity of the titrant, or: calculate how many mol of the titrant was added out of the buret. Check again what exactly was the question. Do de rest of the calculation, and check: the right mol proportion. dilutions the right units (ml, mol, mmol, mg, l, ml, etc.)

Determine by titration with thio how many g of Iodine is dissolved in a liter of tri Iodine solution.
Determine the concentration of acetic acid in vinegar, by titration with 0.1M KOH. Knowing that the acetic acid is rather concentrated, you must first dilute it with a factor of exactly 10. After that, you titrate ten ml of the diluted vinegar.
According to the law, vinegar must contain at least 4 g of acetic acid per 100 ml vinegar; check the investigated vinegar: does it respect the law?
Weigh exactly about 2.7 g cristal soda: (Na₂CO₃.xH₂O)
Add some drops of methyl red + 1M HCl from a buret until clear color change to red (clearly passing the equivalence point, you added too much!) Now heat the solution to remove all CO₂.
After that you must titrate (back) with 0.1M KOH. Use a pH meter, read th pH value every time after adding 0.5 ml titrantliquid and make a graph on graph paper.
Then calculate x and also how much cristal water is present in half a kilo of soda.
The molarity of oxalic acid(aq) can be determined in two ways by titration:
1. with 0.1M Potassium permanganate. You must also add some acid (1M sulfuric acid) and heat softly at the start of the titration.
2. with 0.1M KOH.
The ammonia concentration in a cleaner can be determined through titration with 0.1M HCl; the end point can be found with a conductometer.
Write after every half ml titrant the conductibility of the solution and make a graph.
Determine the amount of vitamine C in a vitamine C tablet.

Action task D: Buffer mixtures

According to the points I - III you must work in groups and prepare and controll three buffer mixtures. For preparing you can chose from six substances and those three substances must be mixed in the right mol proportions.	Every time when working, you must write down all you do, observe, think about the procedure. At the end a report must me made. Take care that the substance to investigate always remains in stock; never use all of it! Draw conclusions of every observation; that's how a lot of research will turn out to be unnecessary.
The 3 action points for every task are:	The 6 tasks are:
Make the buffer mixture in a volume of about 100 ml and with a buffer capacity of 1 mol/l. Calculate the pH with the bufferformula and check your calculation by measuring that pH with a pH meter or with pH-paper. Devide the buffer mixture in two parts of about 50 ml.	Ammonium chloride Acetic acid Ammonia Sodium monoHydrogen phosphate Sodium acetate Sodium diHydrogen phosphate