Zuur-base berekeningen

Zowel in de industrie als in laboratoria worden veel zuur-base-reacties toegepast. Altijd moet er dan onderzocht worden hoeveel van elk moeten worden samengevoegd, welke zuurtegraad nodig is, hoe neutraal een oplossing moet of mag zijn, enzovoort.
Geen wonder dus dat in deze module het rekenen met zuurtegraad, met pH, met pKa of pKb, of zelfs ook met bufferoplossingen, niet mag ontbreken.

De belangrijkste reden om p-waarden te gebruiken is dat we vaak concentraties toepassen van zeer verdunde oplossingen.
Het is veel gemakkelijker te zeggen: pH = 6 dan [H₃O⁺] = 10^-6 mol/l.
Vergeet alsjeblieft nooit dat een hoge p-waarde automatisch betekent een zeer kleine overeenkomstige werkelijke waarde.
pOH = 9 (nogal een hoge waarde) betekent dus een lage concentratie van OH^--ionen:
pOH = 9 → [OH^-] = 10^-9 mol/l
Als je iets zegt of schrijft over concentraties kan de eenheid mol/l (mol per liter) niet ontbreken; gebruik je de p-waarde, dan heb je helemaal geen eenheid nodig. Maar bedenk wel dat die is gebaseerd op de bekende eenheid mol/l

Ter herinnering: in water met een normale temperatuur (zeg maar 20 - 25ºC) geldt: pH + pOH = pK_W = 14

Dus, zodra je de pH kent, ken je ook de pOH.

Een wateroplossing heet NEUTRAAL als pH = pOH, bij welke temperatuur dan ook. Dat is het belangrijkste criterium voor een neutrale oplossing. Het staat gelijk aan de uitspraak: de concentraties van H₃O⁺ en OH^- zijn gelijk.

Toevoeging van zuur aan een oplossing betekent dat de pH-waarde lager wordt en de p-OH-waarde wordt hoger.
Toevoeging van base betekent een hogere pH en een lagere pOH.

De waarden van pH kunnen ook gebroken getallen zijn, zoals 3,4 en 10,7 e.d. Dat kan de wiskundige berekeningen bemoeilijken.
Bijvoorbeeld: als de pH=3,5 dan is de concentratie [H₃O⁺] gelijk aan 10^-3,5mol/l.
Maar vaak accepteren we geen gebroken exponenten.
Je moet meteen zien en begrijpen dat in het voorbeeld de concentratie dus ergens moet liggen tussen de waarden 10^-3 en 10^-4mol/l (want de pH ligt tussen 3 en 4).
Een goede rekenmachine geeft natuurlijk meteen de oplossing, maar zelfs zonder die machine moet je de berekening kunnen uitvoeren:

[Let op: log3=0,5]
pH = 3,5 = 4 – 0,5     →       -log[H₃O⁺] = 4 - 0,5     →       [H₃O⁺] = 3 x 10^-4 mol/l.

0,1M HAc wil zeggen: 0,1 mol azijnzuur (CH₃COOH) werd in water opgelost tot één liter.
Een deel van de zuurmoleculen dissocieert in H⁺ en Ac^-.
De hoeveelheid van H⁺ (in water H₃O⁺) bepaalt de waarde van de pH (=-log[H₃O⁺]).
We moeten deze hoeveelheid H⁺ kennen, evenals de sterkte/zwakte van het zuur, dus de K_A
We consulteren de tabel om te zien dat K_A = 10^-4 of pK_A = 4



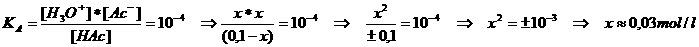
We weten dat HAc zwak zuur is. De waarde van x zal dus behoorlijk klein zijn in vergelijking met [HAc]
of ook kun je zeggen: x is verwaarloosbaar t.o.v. [HAc].
Dus: 0,03 mol HAc dissocieerde in ionen     → [H₃O⁺] = 0,03 = 3 x 10^-2 mol/l     →       pH = 2-log3 = 1,5

Nooit vergeten:

hoe zwakker een zuur, hoe kleiner K_A

en

hoe sterker een zuur, hoe groter K_A


Sterke zuren en basen in de tabel hebben geen bepaalde K-waarde.


De manier waarop je te werk moet gaan is bij elke vraagstuk als volgt:

1. Zorg er voor dat je precies weet hoeveel zuur er gebruikt wordt
2. Zorg er voor dat je precies weet hoeveel base er begruikt wordt
3. Onderzoek m.b.v. een kloppende reactievergelijking welke van de twee op gaat en van welke wat over blijft
4. Bereken hoeveel er overblijft en reken dit om naar een liter
5. Hou voortdurend in de gaten met welke volumes je werkt