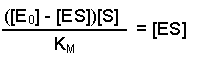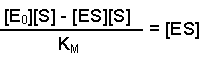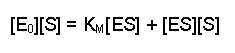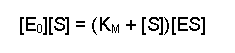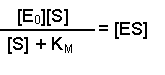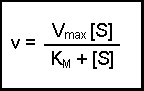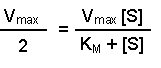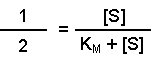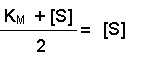Anexo em InglÍs sobre Michaelis Menten
http://www.le.ac.uk/by/teach/biochemweb/tutorials/michment2print.html
Enzyme kinetics and the Michaelis-Menten equation
Introduction
Study of the impact made on the rate of an enzyme-catalysed reaction by changes in experimental conditions is known as enzyme kinetics. Knowledge of kinetics can be a very useful tool in understanding the mechanism by which an enzyme carries out its catalytic activity.
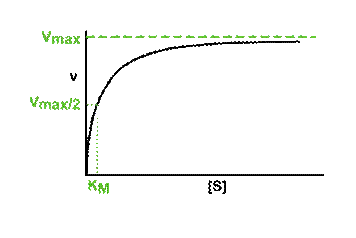
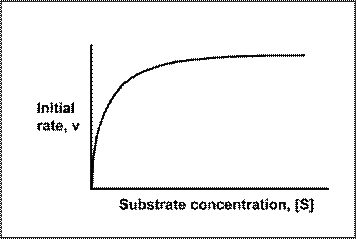
The effect of substrate concentration on the initial rate of an enzyme-catalysed reaction is a central concept in enzyme kinetics. When data are generated from experiments of this type and the results plotted as a graph of initial rate (v, y-axis) against substrate concentration ([S] *, x-axis), many enzymes exhibit a rectangular hyperbolic curve like the one shown in the diagram below.
*Note: the use of square brackets, as for [S] above is short-hand notation for "concentration of S", a convention that will be used extensively in the derivation below.
Observations of this type set Leonor Michaelis and Maud Menten thinking about the underlying reasons why a curve should follow this shape and led them to derive an algebraic equation that now bears their names. There are several modern ways to explain the way in which the Michaelis-Menten equation is derived, and one is spelt out below.
Deriving the Michaelis-Menten Equation
Start with the generalised scheme for enzyme-catalysed production of a product (P) from substrate (S). The enzyme (E) does not magically convert S into P, it must first come into physical contact with it, i.e. E binds S to form an enzyme-substrate complex (ES).
Michaelis and Menten therefore set out the following scheme:
The terms k1, k-1 and k2 are rate constants for, respectively, the association of substrate and enzyme, the dissociation of unaltered substrate from the enzyme and the dissociation of product (= altered substrate) from the enzyme. Note that there is the theoretical possibility of a reverse reaction, with ES complex forming from E and P, but this can be ignored because we are considering initial rates of reaction, i.e. when the enzyme is first provided with substrate, so there should not be any product available to combine with enzyme.
The overall rate of the reaction (v) is limited by the step ES to E + P, and this will depend on two factors - the rate of that step (i.e. k2) and the concentration of enzyme that has substrate bound, i.e. [ES]. This can be written as:
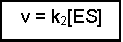
(Equation 1)
At this point it is important to draw your attention to two assumptions that are made in this scheme. The first is the availability of a vast excess of substrate, so that [S]>>[E]. Secondly, it is assumed that the system is in steady-state, i.e. that the ES complex is being formed and broken down at the same rate, so that overall [ES] is constant. The formation of ES will depend on the rate constant K1 and the availability of enzyme and substrate, i.e. [E] and [S]. The breakdown of [ES] can occur in two ways, either the conversion of substrate to product or the non-reactive dissociation of substrate from the complex. In both instances the [ES] will be significant. Thus, at steady state we can write:
The next couple of steps are rearrangements of this equation. First of all we can collect together the rate constants on the right-hand side because they are both multiplied by [ES], this gives us:
Then dividing both sides by (k-1 + k2), this becomes:
Notice that the three rate constants are now on the same side of the equation. As the name implies, these terms are constants, so we can actually combine them into one term. This new constant is termed the Michaelis constant and is written KM.
Notice that the three rate constants in the definition of KM are actually inverted (the other way up) compared with our previous equation. This is a 'trick' that makes for easier calculation at a later stage. Substituting this definition of KM into our previous equation now gives us:
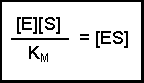
(Equation 2)
The total amount of enzyme in the system must be the same throughout the experiment, but it can either be free (unbound) E or in complex with substrate, ES. If we term the total enzyme E0, this relationship can be written out:
This can be rearranged (by subtracting [ES] from each side) to give:
So, the [E] free in solution is equal to the total amount of enzyme minus the amount that has substrate bound. Substituting this definition of [E] back into equation 2 gives us:
This can now be rearranged in several steps. First of all, open the bracket so that the terms [E0] and [ES] are separately multiplied by [S]
Next, multiply each side by KM, this gives us:
Then collect the two [ES] terms together on the same side (you can either think of this as adding [ES][S] to both sides or as 'carry over and change the sign' - your preference will probably be an indication of how long ago you went to school). This gives:
Then because both terms on the right-hand side are multiplied by [ES] we can collect them together into a bracket:
Dividing both sides by (KM + [S]) now gives us:
Substituting this left-hand side into Equation 1 in place of [ES] results in:
The maximum rate, which we can call Vmax, would be achieved when all of the enzyme molecules have substrate bound. Under conditions when [S] is much greater than [E], it is fair to assume that all E will be in the form ES. Therefore [E0] = [ES]. Thinking again about Equation 1, we could substitute the term Vmax for v and [E0] for [ES]. This would give us:
Notice that k2[E0] was present in our previous equation, so we can replace this with Vmax, giving a final equation:
This final equation is actually called the Michaelis-Menten equation.
So what?
Perhaps this derivation still leaves you puzzled about the importance of the Michaelis-Menten equation. The significance becomes clearer when you consider the case when the rate of reaction (v) is exactly half of the maximal reaction rate (Vmax). Under those circumstances, the Michaelis-Menten equation could be written:
On dividing both sides by Vmax this becomes:
Multiplying both sides by (KM + [S]) gives:
And then multiplying both sides by 2 further resolves the equation to:
2[S] on the right-hand side is the same as [S] + [S], so we can take away one [S] from each side. Thus when the rate of the reaction is half of the maximum rate:
The KM of an enzyme is therefore the substrate concentration at which the reaction occurs at half of the maximum rate. If we now reconsider the graph that came at the start of this tutorial it could be written:
What does this all mean in physical terms? KM is an indicator of the affinity that an enzyme has for a given substrate, and hence the stability of the enzyme-substrate complex.
Look at the shape of the graph. At low [S], it is the availability of substrate that is the limiting factor. Therefore as more substrate is added there is a rapid increase in the initial rate of the reaction - any substrate is rapidly mopped up and converted to product. At the KM, 50% of active sites have substrate bound. At higher [S] a point is reached (at least theoretically) where all of the enzyme has substrate bound and is working flat out. Adding more substrate will not increase the rate of the reaction, hence the levelling out observed in the graph.
There are limitations in the quantitative (i.e. numerical) interpretation of this type of graph, known as a Michaelis plot. The Vmax is never really reached and therefore Vmax and hence KM values calculated from this graph are somewhat approximate. A more accurate way to determine Vmax and KM (though still not perfect) is to convert the data into a linear Lineweaver-Burk plot. See separate page:
"Experimental calculation of Vmax and KM "
If, incidentally, we consider that the rate constant k2 for the conversion of ES to E + P in the initial scheme is the step determining the overall rate of production of P (as we have in deriving the Michaelis-Menten equation) then k2 is actually the same term as kcat, the turnover number.
voltar ao curso


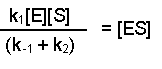
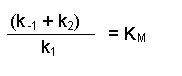
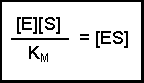 (Equation 2)
(Equation 2)